Is there a source out there for files that have all unique numbers for different number bases?
I generated my own for base 10 by having 10 nested loops and a humungous IF statement that checked for uniqueness each time the inmost loop incremented. The resulting 10 digit number did not contain a duplicate number. If none of the numbers were dup’d, I’d write it to a file. But going up the Base 12 increases that effort immensely. At least in computer “crank” time. Is there an efficient way to generate all numbers of a certain base with no repeated digits in the string?
It seems something like that - the files of unique numbers for each number base - should be living on the internet somewhere.
For clarity, with Base 10, this number would be what I wanted 3572109864
This number would not: 3572103864 because there are two “3’s”.
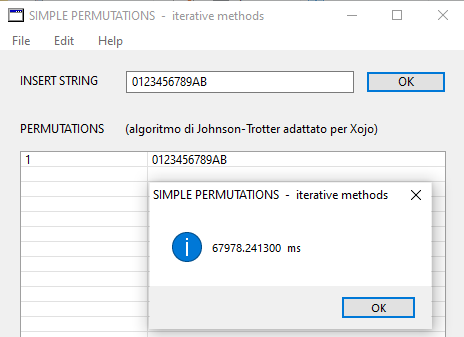
I’m looking for the same thing but with Base 12 numbers 0123456789AB
Or a more efficient algorithm besides 12 nested loops running from 0 to 11, converting 10 and 11 to A and B and checking that no number has a repeated 12 digit number has repeated “digits” - A and B are digits so each number is converted to text and each element is compared to all the others.
 . I am really just focusing on BASE 12 now.
. I am really just focusing on BASE 12 now.
 What did Jim Cary say in Mask … “Somebody stop me!”
What did Jim Cary say in Mask … “Somebody stop me!”