Line Crossing a hexagon grid

[Enric_Herrera]

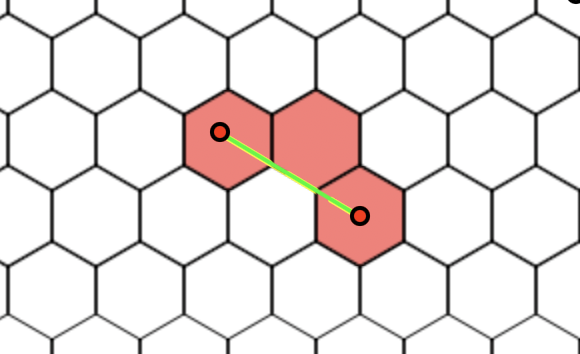
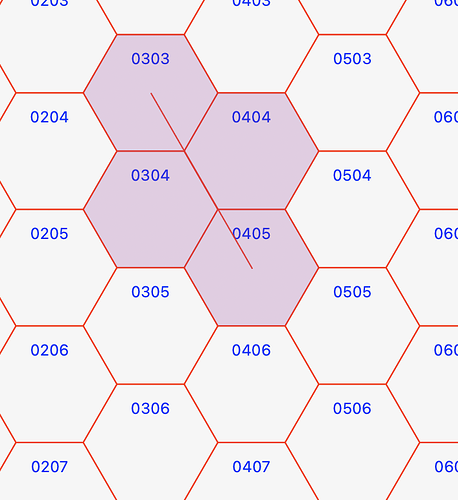
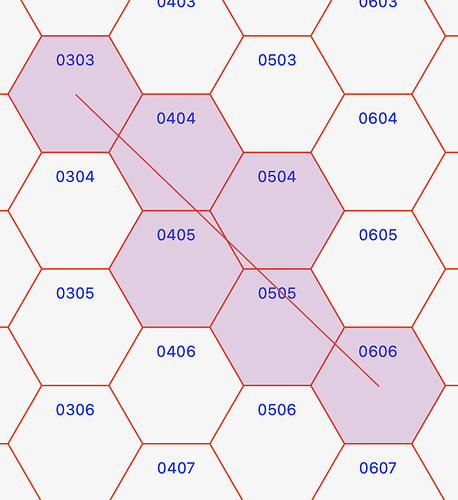
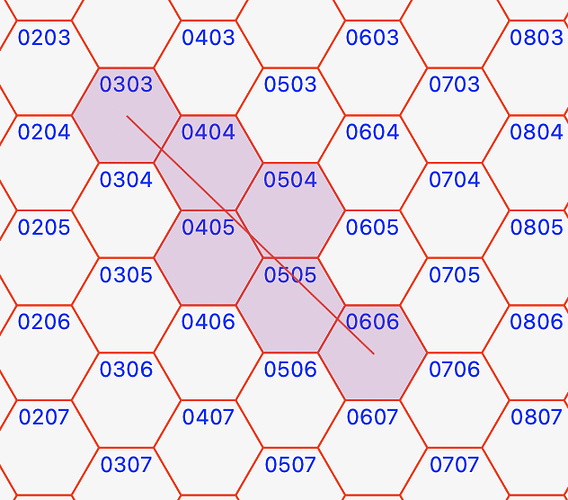
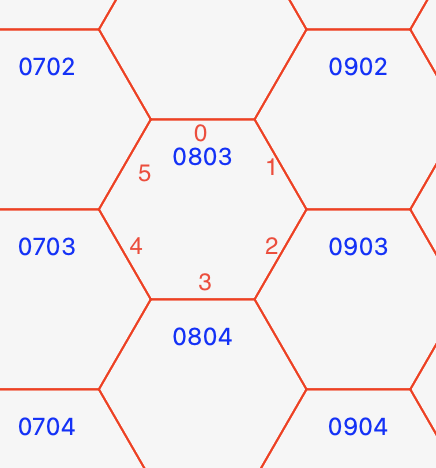
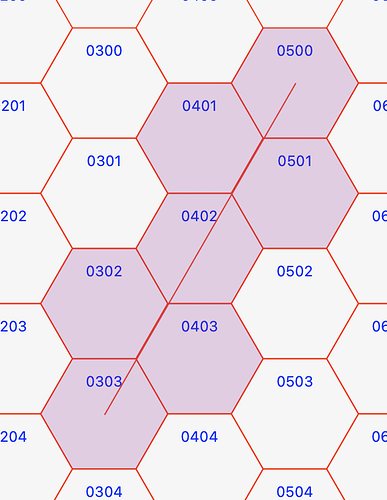
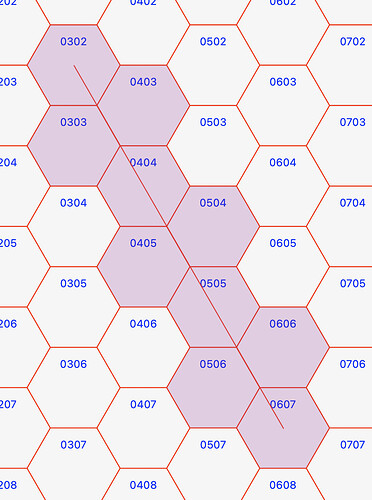
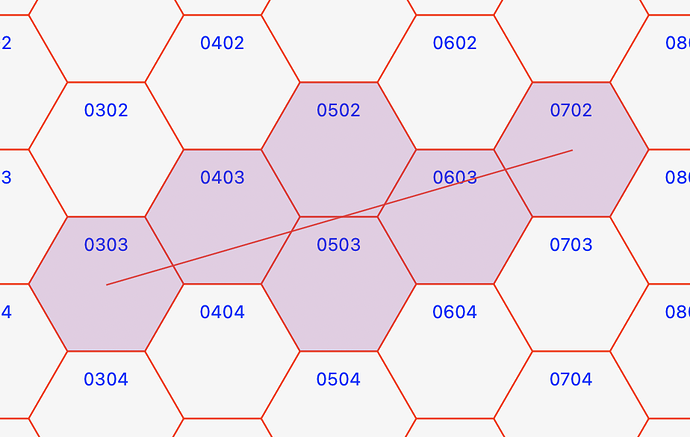
We have an array of hexagons that a line, from the center of a starting hexagon goes to the center to a target hexagon (this works well).
The start hex and target hex centers are:
Var p1 As Point = GetCenter(from)
Var p2 As Point = GetCenter(tohex)

For each hexagon in the array we get its center and call GetHexagonEnteringSide
to get the side of the hexagons from where the line enters to the hex.

Var hexagon As Point = GetCenter(hex)

Public Function GetHexagonEnteringSide(p1 As Point, p2 As Point, hexagon As Point) As Integer
  ' Define Pi
  Const Pi = 3.14159265358979323846264338327950
  
  ' Calculate the vector representing the line
  Var lineVector As New Point(p2.X - p1.X, p2.Y - p1.Y)
  
  ' Calculate the vector representing the hexagon center to the starting point
  Var hexagonToStartVector As New Point(p1.X - hexagon.X, p1.Y - hexagon.Y)
  
  ' Calculate the angle between the line vector and the hexagonToStartVector
  Var angle As Double = Atan2(lineVector.Y, lineVector.X) - Atan2(hexagonToStartVector.Y, hexagonToStartVector.X)
  
  ' Normalize the angle to be within [0, 2 * Pi)
  If angle < 0 Then angle = angle + 2 * Pi
  
  ' Determine the hexagon entering side based on the normalized angle
  Var enteringSide As Integer = 1 +  round(angle / (Pi / 3)) Mod 6
  
  ' Return the entering side
  Return enteringSide
End Function

But, something is not working and I can’t find what is it. The resulting entering side is not correct always and I do not have enough skills on Vectors, angles, etc.
Can anyone give some light ?.

[Robert_Livingston]

Perhaps you could sketch a diagram of what you are trying to define and include this in the query.

You have two vectors that are defined as points.? Where is the origin of these vectors? Is it the same origin?

“hexagon in the array”? That happen to lie between the “start” hexagon and the “target” hexagon. Are these regular hexagons tiled on a plane?

Why is the vector representing the line simply the midpoint of the line?

Speaking only for myself, I have difficulty visualizing what is being asked.

[RudolfJ]

Examble: Test-line

https://www.dropbox.com/scl/fi/l314s37g8k3d98zolch3n/hexagon-6Eck-test-3.xojo_binary_project?rlkey=a2t5gt7sz42ayc00xrzgecton&dl=1

[RudolfJ]

New sorry Picture
https://www.dropbox.com/scl/fo/xwg2d316fs8edsjomyt9l/h?rlkey=acity2om5vvli5k3sr1klrqhr&dl=1

[RudolfJ]

Now with Pixmapshape collision

https://www.dropbox.com/scl/fo/a7cwj38fms2tg069i2k0l/h?rlkey=7rjypx8kvbudoupwv2zmecrzf&dl=1

[Enric_Herrera]

Thanks Robert and Rudolf I’ll try to clarify my project.
I’m using flat-topped hexagon grid, odd columns down

The Rudolf example is near my project.
In my case a line goes from the center of the started hexagon to the center of the target hexagon. Always from center to center. Then all hexagons crossed by the line are highlighted.

When the line crosses exactly a side of two hexagons both are highlighted.

When crossing the border of two hexes, both are included

I use zoom and scroll

I need to know the side of each involved hexagon crossed by the line.

In the last example the line enters
0404 from 5
0405 from 0
0504 from 4
0505 from 0
and reaches 0606 from 5

Getting these sides from code is where I’m lost.

[Enric_Herrera]

A simple way I tried was using GetSharedSide()
That works on all cases where the line not goes through a common
border.

Public Function GetSharedSide(fromHex as string, toHex as string) As string
  // tornem  el borde del from hex
  // Si es vol el borde del toHex cal cridar intercanviant els hexes (tohex, fromHex)
  // 
  // ODD column DOWN LAYOUT
  
  Var colFrom  as Integer = fromHex.left(2).Val
  Var colTo as integer = toHex.left(2).val
  Var rowFrom as integer = fromHex.Right(2).val
  Var rowTo as integer = toHex.Right(2).val
  
  if not(AreAdjacent(fromHex, toHex)) then
    return "-1"
  end if
  
  // Mateixa columna
  if colFrom = colTo then
    if rowFrom > rowTo then return "0" else return "3"
  end if
  
  if colFrom mod 2 = 0 then // columna PAR **********
    
    // cap a l'oest
    if colFrom > colTo   then
      if rowFrom = rowto then Return "4" else Return "5"
    end if
    // cap a l'est
    if colFrom < colTo  then
      if rowFrom = rowto then Return "2" else Return "1"
    end if
    
  else // Columna impar **********
    
    // cap a l'oest
    if colFrom > colTo  then
      if rowFrom = rowto then Return "5" else  Return "4"
    end if
    // cap a l'est
    if colFrom < colTo   then
      if rowFrom = rowto then Return "1" else Return "2"
    end if
  end if
  
  return "-1"
End Function

LosHexes() is the array of all involved hexes
And to test it

Public Sub TestBorders()
  var index as integer = 0
  var hex1, hex2 as string
  var border as string
  
  For i as integer = 0 to LosHexes.LastIndex-1
    hex1 = LosHexes(i)
    hex2 = LosHexes(i+1)
    border = GetSharedSide(hex2,hex1)
    system.DebugLog (hex2 + "-"+ border )
  Next
End Sub

This works except (that’s the point) when the line crosses exactly the common border of two hexagons. For these cases I tried the vector system that I do not understand well and not works either.
for example:

[Robert_Livingston]

// Calculate the vector representing the hexagon center to the starting point
 Var hexagonToStartVector As New Point(p1.X - hexagon.X, p1.Y - hexagon.Y)

Why isn’t this:

Var hexagonToStartVector As New Point(hexagon.X - p1.X, hexagon.Y - p1.Y)

This would seem more in keeping with

// Calculate the vector representing the line
Var lineVector As New Point(p2.X - p1.X, p2.Y - p1.Y)

[Robert_Livingston]

Const Pi = 3.14159265358979323846264338327950
// Assume that the upper horizontal side is 0 and then numbered clockwise 1, 2 etc.
// Basically setting up a coordinate system where the center of the startHexagon is considered the origin
Var p1 As New Point
Var p2 As New Point
Var hexagon As New Point
Var side As Integer

Var startToEndVector As New Point
startToEndVector.X = p2.X - p1.X
startToEndVector.Y = p2.Y - p1.Y
Var startToEndAngle As Double
startToEndAngle = ATan2(startToEndVector.X, startToEndVector.Y)

Var startToHexagonVector As New Point
startToHexagonVector.X = hexagon.X - p1.X
startToHexagonVector.Y = hexagon.Y - p1.Y
Var startToHexagonAngle As Double
startToHexagonAngle = ATan2(startToHexagonVector.X, startToHexagonVector.Y)

// The special cases when the connecting line runs exactly across a common border
// the possible startToEndAngle angles are 0, Pi/3, 2Pi/3, Pi, 4Pi/3, 5Pi/3

If startToEndAngle.Equals(0, 10) Then
  If startToHexagonAngle > startToEndAngle Then side = 3 Else side = 0
  
ElseIf startToEndAngle.Equals(Pi / 3, 10) Then
  If startToHexagonAngle > startToEndAngle Then side = 2 Else side = 5
  
ElseIf startToEndAngle.Equals(2 * Pi / 3, 10) Then
  If startToHexagonAngle > startToEndAngle Then side = 4 Else side = 1
  
ElseIf startToEndAngle.Equals(Pi, 10) Then
  If startToHexagonAngle > startToEndAngle Then side = 0 Else side = 3
  
ElseIf startToEndAngle.Equals(4 * Pi / 3, 10) Then
  If startToHexagonAngle > startToEndAngle Then side = 5 Else side = 2
  
ElseIf startToEndAngle.Equals(5 * Pi / 3, 10) Then
  If startToHexagonAngle > startToEndAngle Then side = 1 Else side =4
  
Else
  MessageBox("It is not one of the special case")
End If

I would treat the situation where

when the line crosses exactly the common border of two hexagons.

As a special case and use code like the above to deal with this special case.

[Enric_Herrera]

You’re right Robert, startVector should be calculated as:

Var hexagonToStartVector As New Point(hexagon.X - p1.X, hexagon.Y - p1.Y)

But I’m still having a big problem when line passes exactly through the border. This happens when the line is horizontal or NE, NW, SW, SE. Some hexagons have, in this case, two borders touched by the line.

The example from 0303 to 0405 gives those entering borders:
11:05:14 : PB Launched
11:05:25 : 0304-0
: 0404-4
: 0405-0
Assuming 0 is the hexagon top side

The results are correct but insufficient because 0304 should have also border 1 touched by the line, and 0404 the same, so the result should be:

0304 - 0 and 1
0404 4 and 5
0405 0 and 5

[Ivan_Tellez]

@Enric_Herrera

But I’m still having a big problem when line passes exactly through the border.

Can you aply a little offset to the centers just when doing your calculations? a little to the left for the starting point and to the right for the ending one.

[Enric_Herrera]

Can you aply a little offset to the centers just when doing your calculations? a little to the left for the starting point and to the right for the ending one.

This is a major change, I should call five times the method that gets the crossed hexagons, one for the normal center to center then four other cases with displacing the y +/- delta and displacing the x +/- delta.

var delta as integer = 4
for offset as integer = 0 to 4
' 0 normal call
if offset = 1 then 
  p1.y = p1.y+delta
elseif offset = 2 then 
  p1.y = p1.y-delta
elseif offset = 3 then 
  p1.x = p1.x+delta
elseif offset =4 then  
  p1.x = p1.x-delta
end if
End for

Then the array that keeps the hexes crossed must be changed to accept same hex with diferent border.

Private Sub AddToArray(x as integer, y as integer)
  Var row, col as integer
  x = x + mw.HorizontalScrollBar.Value
  y = y + mw.VerticalScrollBar.Value
  mw.BoardMap.PointToHex(x,y,row,col)
  var hex as string = Terrain.RowColToHex(row,col)
  
  if LosHexes.IndexOf(hex) = -1 then
    LosHexes.Add hex
  end if
End Sub

It’s a possibility, not seems the most elegant, but I’ll try this in a separate project.

[Robert_Livingston]

But not 0304 - 2 ?
But not 0404 - 3 ?

[Robert_Livingston]

I think I understand your definition of “enter side”.

Basically, we are going to identify the “special” circumstances that result in a connecting line between the start and the end hexagons that runs exactly through the common side of two adjacent hexagons.

Then divide the special cases into the 6 relevant directions (NE, NW, SE, SW, WEST, EAST) and for each one considered separately write the code that places the “enter side” into a data structure that is created for this purpose (a dictionary) of all the titled hexagons.

// Screw trigonometry functions
// dealing with the special case of the connecting line passes exactly through borders
Const VERY_SMALL As Double = .000001

Var distanceStartEnd As Double
// the side of a hexagon is the unit distance (1) 

// Example values for the start and end hexagon are provided.
Var rStart, cStart As Integer // row and column of the start hexagon
Var rEnd, cEnd As Integer // row and column of the end hexagon
rStart = 7
cStart = 6
rEnd = 2
cEnd = 3

// We are defining a side of a hexagon as having the unit value 1
// This will be the distance between the centers of the example hexagons
distanceStartEnd = 9 // in this example case

Var iDistanceStartEnd As Integer

// identify whether these start and end hexagons are a special case with connecting line passing exactly through borders
Var qualify As Boolean // does it qualify as a special case?

iDistanceStartEnd = Round(distanceStartEnd)
// should be an integer value if the side is considered to be 1
If Abs(iDistanceStartEnd - distanceStartEnd) < VERY_SMALL Then qualify = True Else qualify = False

// The distances should be a multiple of 3 between qualifying end and start hexagons.
If iDistanceStartEnd Mod 3 = 0 And qualify Then
  qualify = True
Else
  qualify = False
End If

// now figure out the "entry" sides for the involved hexagons between the start and end hexagon.
If qualify Then // the start/end pair of hexagons qualify
  
  // the angled directions
  Var NW, NE, SE, SW, WEST, EAST As Boolean
  
  If rStart > rEnd And cStart > cEnd Then
    NW = True
  End If
  If rStart > rEnd And cStart < cEnd Then
    NE = True
  End If
  If rStart < rEnd And cStart > cEnd Then
    SW = True
  End If
  If rStart < rEnd And cStart < cEnd Then
    SE = True
  End If
  If rStart = rEnd And cStart > cEnd Then
    WEST = True
  End If
  If rStart = rEnd And cStart < cEnd Then
    EAST = True
  End If
  
  Var totRow, totCol As Integer // whatever values fill the case at hand. - Example
  totRow = 8
  totCol = 8
  // Var hex(-1, -1) As Integer
  // hex.ResizeTo(totRow, totCol)
  
  Var theValue As String
  
  // create a structure (a dictionary) that will hold all the "entry sides" for a given hexagon
  // dHex.Value("05*04") might be "3-4"
  Var dHex As New Dictionary
  Var sRow, sCol As String
  For nRow As Integer = 0 To totRow
    sRow = Format(nRow, "00")
    
    For nCol As Integer = 0 To totCol
      sCol = Format(nCol, "00")
      theValue = sCol + "*" + sRow
      dHex.Value(theValue) = ""
    Next nCol
    
  Next nRow
  
  Var incrementRow As Integer // the rows of hexagons on a diagonal increment or decrement in a pattern 1, 2, 1, 2, 1 etc.
  // within a row there is a pattern with (in this example) the even column hexagons are higher than their odd column row members
  Var upHex As Boolean // up or down relative to some others in the row
  
  // NW
  If NW Then
    
    If cStart Mod 2 = 0 Then upHex = True // even columns have "high" rows
    If upHex Then incrementRow = -2 Else incrementRow = -1
    Var jRow As Integer = rStart
    
    For jCol As Integer = cStart To cEnd Step -1
      
      // the hexagon directly above
      sRow = Format(jRow - 1, "00")
      sCol = Format(jCol, "00")
      dHex.Value(sCol + "*" + sRow) = "3" + "-" + "4"
      
      // the hexagon above and to the left
      If upHex Then
        sRow = Format(jRow - 1, "00")
      Else
        sRow = Format(jRow, "00")
      End If
      sCol = Format(jCol - 1, "00")
      dHex.Value(sCol + "*" + sRow) = "1" + "-" + "2"
      
      // move on to the next hexagon with line through its center
      jRow = jRow + incrementRow
      
      upHex = Not (upHex)
      If upHex Then incrementRow = -2 Else incrementRow = -1
      
    Next jCol
    
  End If
  
  // Write similar custom code for each of the other
  // WEST and EAST are simplest, NE, SE, SW are analogous to what has been provided for NW
  // NE
  // SE
  // SW
  // WEST
  // EAST
  
End If

[Enric_Herrera]

Thanks Robert,
That’s right’s you said, I need only the side from where the line ENTER the hexagons.
I’ll study your code and try to replicate for each direction.

[Enric_Herrera]

Hi Robert,

I’ trying to use your code, and just started I’ve a question,

// Example values for the start and end hexagon are provided.
Var rStart, cStart As Integer // row and column of the start hexagon
Var rEnd, cEnd As Integer // row and column of the end hexagon
rStart = 7
cStart = 6
rEnd = 2
cEnd = 3

in your example the hexagons translated to my coordinates system “CCRR”:
0607 to 0302

// We are defining a side of a hexagon as having the unit value 1
// This will be the distance between the centers of the example hexagons
distanceStartEnd = 9 // in this example case

But the distance is 6, and why the side is 1?

(You count how many radius?) so hex 0302 count as 1 but hex 0404 count as 2?
If you count radius, what about the following example:

[Robert_Livingston]

@Enric_Herrera

(You count how many radius?) so hex 0302 count as 1 but hex 0404 count as 2?
If you count radius, what about the following example:

In the special case situation, the distance between 0302 and 0607 is 9. From the center of 0302 to its edge is 1 (the length of a side). The distance from that edge to the edge of 0404 is 1 (the length of a side). The distance across the entirety of 0404 is 2. The distance from the edge of 0404 to the edge of 0505 is 1. The distance across the entirety of 0505 is 2. The distance from the edge of 0505 to the edge of 0607 is 1. The distance from the edge of 0607 to the center of 0607 is 1.

If you add up all these things then you get 9 which is the distance from the center of 0302 to the center of 0607.

---

What about the following example?

Well that is not a special case and that line measurement will be not be a simple integer. It will have to be calculated as the distance between two points:

Sqrt((P0303.X - P0707.X) ^ 2 + (P0303.Y - P0707.Y) ^ 2)

I assumed from your original post that you had already established the Points that define the center of all the hexagons. That work cannot be abandoned.

For the grid of hexagons, the center of one of them will have to be declared as the 0, 0. Let’s say we decide on your first image that the center of 0306 is going to be the 0,0 point. It is easy to establish the center point of 0305. The distance from the center of a hexagon of side = 1 to the center of and edge is

Sqrt(3) / 2 : That is the height of an equilateral triangle of side 1

and for simplicity of reference we will call that h.

The center point of 0305 will be 0, 2 * h. The center point of 0304 will be 0, 4 * h. etc. as you move up the column. How about moving to the next column?

The center point of 0406 is (1.5, h)
The center point of 0407 is (1.5, -h)
The center point of 0405 is (1.5, h + 2 * h) or (1.5, 3 * h)

The center point of 0505 is (3, 2 * h)
The center point of 0504 is (3, 4 * h)

The pattern should become evident. The centers of all the hexagons in the grid can be determined in this coordinate system.

[Robert_Livingston]

Moving on to your second diagram, if we adhere to the coordinate system that we established in my last entry:

The center of 0303 is (0, 6 * h)

The center of 0702 is (6, 8 * h)

The distance between them would be

Sqrt( 6 ^ 2 + (2 * h) ^ 2)

[Robert_Livingston]

In my original post, I failed to deal with the hexagons that are bisected by the line between start and end. I have added the code below to include these.

For jCol As Integer = cStart To cEnd Step -1

// the hexagon itself
sRow = Format(jRow, "00")
sCol = Format(jCol, "00")
dHex.Value(sCol + "*" + sRow) = "2" + "-" + "3"

// the hexagon directly above
sRow = Format(jRow - 1, “00”)
sCol = Format(jCol, “00”)
dHex.Value(sCol + “*” + sRow) = “3” + “-” + “4”

// the hexagon above and to the left
If upHex Then
sRow = Format(jRow - 1, “00”)
Else
sRow = Format(jRow, “00”)
End If
sCol = Format(jCol - 1, “00”)
dHex.Value(sCol + “*” + sRow) = “1” + “-” + “2”

// move on to the next hexagon with line through its center
jRow = jRow + incrementRow

upHex = Not (upHex)
If upHex Then incrementRow = -2 Else incrementRow = -1

Next jCol

// deal with the start hexagon which does not have an entry side(s)
sRow = Format(rStart, "00")
sCol = Format(cStart, "00")
dHex.Value(sCol + "*" + sRow) = "start"

// deal with the end hexagon as you see fit. I am not sure if you track entry side(3)
sRow = Format(rEnd, "00")
sCol = Format(cEnd, "00")
// ?? dHex.Value(sCol + "*" + sRow) = "end"

[RudolfJ]

hello Enric Herrera,
My simple way to determine the direction from the center to the entry point without any major calculations

https://www.dropbox.com/scl/fi/6kzccuqn19gndxw4alrh3/test-direction-Point.xojo_binary_project?rlkey=4d87tiq18rka7s1026vxq47zt&dl=1