Considering that there’s always a trade off between speed and memory usage, you may be better off ditching everything that involves dynamic memory allocation, and simply dimension all of your arrays to fixed sizes, and avoid the use of dynamically allocated objects. For example, use an array of separate x and y doubles rather than creating new point objects.
There’s another thing I noticed which is probably not very significant, but I’ll point it out anyway since I tend to be picky about these kinds of things. Your method of generating random points has a couple of problems. First, the use of random angles and radii will lead to non uniform distribution of points. They will be more dense towards the centre. The following diagram shows this, with the random angle/radius method on the left and a uniform sample rejection method on the right.
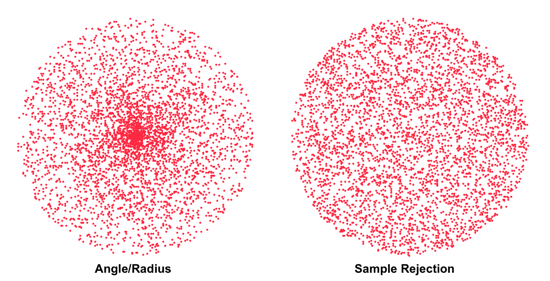
It’s not as bad in your case since you’re generating points that fall outside of the centre area, and so the non-uniformity is not as bad, though it’s still there. The only reliable way to generate uniformly distributed random points over a circular area is to generate random points over a square area that bounds the circle. Then, check to see if the point falls inside the circle. If not, it’s rejected. Because the area of the bounding square is 14% bigger than the area of the circle, it means that 14% of the random points will be rejected. In the case of a circular area, because the sample rejection method avoids the calculation of sin and cos, this often offsets the extra 14% overhead. However, in your case your points are distributed over an annulus rather than a circle, and so the inner points must be rejected as well. In this case 52% of the points will be rejected. So, this may make the sample rejection method too inefficient in this application.
The second problem is where you check to see if the random point falls outside of the bounds of your graphical region. When they do, your program forces them inside. To be statistically correct, these points should be rejected.
The following code uses sample rejection for generating uniform points, and also rejects out of bound points rather than force them within limits. It’s for interest only, because I think it likely runs slower than the original. (I can’t tell with any certainty because the variance between run times seems more dependent on other background tasks.) It also includes a couple of other minor changes that are commented.
#pragma boundsChecking false
#pragma stackOverflowChecking false
#pragma backgroundTasks false
timeTaken = microseconds
dim cellSize as double = minRadius / sqrt( 2 )
dim gridSize as new xojo.core.size( width / cellSize, height / cellSize )
redim locations( -1 )
dim activeList(-1) as xojo.core.point
'R. Weaver 2019-01-17 - Add several new variables for faster distance testing and sample rejection
dim minRadiusSQ As Double = minRadius*minRadius
dim minRadius4 As Double = 4*minRadius
dim minRadius2SQ As Double = 4*minRadiusSQ
// --- Build the neighborhood loop
static neighborhood() as xojo.core.point = array( new xojo.core.point( -1, -1 ), _
new xojo.core.point( 0, -1 ), new xojo.core.point( 1, -1 ), new xojo.core.point( -1, 0 ), _
new xojo.core.point( 1, 0 ), new xojo.core.point( -1, 1 ), new xojo.core.point( 0, 1 ), _
new xojo.core.point( 1, 1 ) )
Dim grid( -1, -1 ) as xojo.core.point // --- Build the grid.
redim grid( gridSize.width, gridSize.height ) // --- we can't use a variable to build it.
Dim p as new xojo.core.point( app.rand.number * width, app.rand.number * height ) // --- Step 1: Set the initial sample
'R. Weaver 2019-01-17 - replace floor and floating point divide with integer divide
'grid( floor( p.x / cellSize ), floor( p.y / cellSize ) ) = p // --- Add to the grid, so it can be checked.
grid( ( p.x \\ cellSize ), ( p.y \\ cellSize ) ) = p // --- Add to the grid, so it can be checked.
activeList.append p // --- Add it to the list of locations to explore next.
samplesCreated = 1
Try // --- Store the location
Dim t as pds2DLoc
t.x = p.x
t.y = p.y
locations.append t
End Try
Dim tooCloseForComfort, addedToGrid as boolean
Dim gridLoc, compareLoc, cSample as pds2DLoc // --- Using structures instead of objects, we improved performance.
Dim rndIdx, iteration, fnsm as integer
Dim radii, angle as double
Dim listCount as integer = actiVeList.ubound
do
rndIdx = app.rand.number * ( listCount + 1 ) // --- Pick a random item from the list of locations to explore
p = activeList( rndIdx )
addedToGrid = false
For iteration = 1 to k // --- Create k samples from our randomly selected existing point.
'R. Weaver 2019-01-18 - Replace angle/radius random point generation
'with uniform distribution sample rejection method
'Original code:
'angle = 0.01745329252 * ( rnd * 361 ) // --- Random direction
'radii = ( rnd * minRadius ) + minRadius // --- Random distance within minRadius & 2minRadius
'cSample.x = ( radii * cos( angle ) ) + p.x
'cSample.y = ( radii * sin( angle ) ) + p.y
'
'// --- Make sure the sample is within bounds.
'
'if cSample.x < 0 then cSample.x = 0
'if cSample.x > width then cSample.x = width
'if cSample.y < 0 then cSample.y = 0
'if cSample.y > height then cSample.y = height
'Sample rejection code
dim x,y,xySQ As Double
do
x=rnd-0.5
y=rnd-0.5
xySQ=x*x+y*y
loop until xySQ<0.25 and xySQ>0.0625
cSample.x=x*minRadius4 + p.x
cSample.y=y*minRadius4 + p.y
'R. Weaver 2019-01-17 - replace floor and floating point divide with integer divide
'gridLoc.x = floor( cSample.x / cellSize ) // --- Obtain the location on our grid.
'gridLoc.y = floor( cSample.y / cellSize )
gridLoc.x = ( cSample.x \\ cellSize ) // --- Obtain the location on our grid.
gridLoc.y = ( cSample.y \\ cellSize )
'R. Weaver 2019-01-18 - Replaces limit conditioning (above) with array index check
'and reject the point rather than force it within bounds
if gridLoc.x<0 or gridLoc.x>gridSize.Width or gridLoc.y<0 or gridLoc.y>gridSize.height then Continue
if grid( gridLoc.x, gridLoc.y ) <> nil then continue // --- if there's already one in here, we can skip this sample.
// --- Now we check our neighbors to make sure that our sample is minRadius away from neighbors at home.
tooCloseForComfort = false
For fnsm = 0 to 7
compareLoc.x = gridLoc.x + neighborhood( fnsm ).x
compareloc.y = gridLoc.y + neighborhood( fnsm ).y
// --- It's this location is out of bounds then skip to the next neighbor.
if ( compareLoc.x < 0 or compareLoc.x >= gridSize.width ) or ( compareLoc.y < 0 or compareLoc.y >= gridSize.height ) then continue
// --- If no neighbor is home, then skip to the next neighbor.
if grid( compareLoc.x, compareLoc.y ) = nil then continue
// --- If we're too close to the neighbor, we reject this sample and move to the next.
'R. Weaver 2019-01-17 - remove sqrt and abs functions and replace minRadius with minRadiusSQ
'if minRadius > sqrt( ( abs( cSample.x - grid( compareLoc.x, compareLoc.y ).x ) ^ 2 ) + ( abs( cSample.y - grid( compareLoc.x, compareLoc.y ).y ) ^ 2 ) ) then
if minRadiusSQ > (( cSample.x - grid( compareLoc.x, compareLoc.y ).x ) ^ 2 ) + (( cSample.y - grid( compareLoc.x, compareLoc.y ).y ) ^ 2 ) then
tooCloseForComfort = true
exit
end if
Next
if not tooCloseForComfort then // --- so we're cool with our neighbors.
grid( gridLoc.x, gridLoc.y ) = new xojo.core.point( cSample.x, cSample.y ) // --- Add to the grid, so it can be checked.
activeList.append grid( gridLoc.x, gridLoc.y ) // --- Add it to the list of locations to explore next.
addedToGrid = true
Dim n as pds2DLoc // --- Store the location
n.x = cSample.x
n.y = cSample.y
locations.append n
end if
Next
samplesCreated = samplesCreated + k
if not addedToGrid then activeList.remove rndIdx // --- We couldn't place any more samples for this item, so we drop it.
listCount = activeList.ubound
Loop until listcount = -1
timeTaken = microseconds - timeTaken

