I must say it’s kind of weird to put 0 0 top left when we are doing mathematics when it is pretty much universal to have 0 at centre right. I didn’t realise that xojo is written with html as the primary context.
Your conversation is going over my head a bit now, but clockwise is clockwise everywhere. And start and end are universal and easily swapped in code, so why is the boolean value even there? In the way it works here, it is fighting against those two standard values…
As far as I’m aware, all software for writing to computer screens uses that coordinate system. I don’t know how this standard was established, but there it is. Xojo is just following that standard. And what does html have to do with it?
You said:
All screen coordinates have 0,0 at the top lefthand point on the screen or window or object. This is not only true in Xojo, all HTML is the same.as though they are analogous.
I am not saying it is wrong, I am just surprised that’s all.
You need the boolean to specify which direction the drawing is taking place from the start angle to the end one. It is convenient.
You could also have only clockwise drawing and switch the starting angle and the end one when needed, but I think it is better having the option to specify the direction.
Like Tim said, that’s very common in the computer world (not only for programming languages).
Try: “This is not only true in Xojo, all HTML is the same, too”.
or: “This is not only true in Xojo, but all HTML is the same, too”.
It’s true in Xojo, it’s true in HTML web pages, and AFAIK all other software that puts stuff in a window where you have to place things relative to the window. I suspect it’s because when you resized a window, on the Mac you used to have to grab the bottom right corner to do so. This goes back to the days before Windows, and before X.
After all, at least with Western script, text grows downwards and to the right.
Either I am not understanding this properly or something is wrong with clockwise vs start/end…
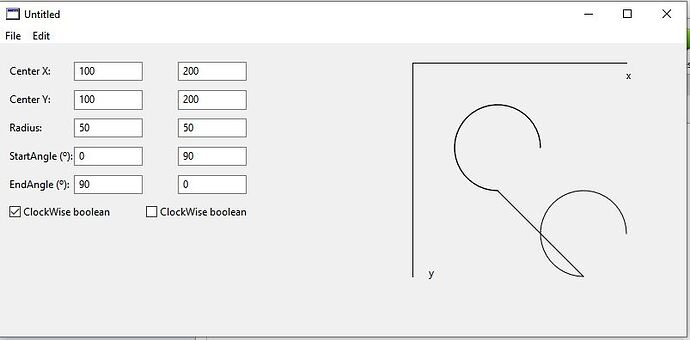
In sample 1, the line linking the two goes correctly from the end of 1 to the start of 2.
One is supposedly clockwise… and the second is supposedly anticlockwise. But the start/end order contradicts that.
So I tried to make 2 arcs, (looking just as they do in example 2) drawing clockwise from the top, joining to another, also drawing clockwise from the top.
My result visually is what I wanted, but according to the boolean value they are not clockwise. According to the start/finish they are clockwise…
Please help me understand how this is correct behaviour. I can only presume that the Boolean value is badly named and should be “reversed”, rather than clockwise/anticlockwise.
Code for tester: Dropbox - xojo shared - Simplify your life
(Note: I am novice with Xojo, but I believe I have the code correct)
I hope this makes sense to you as it did make sense to me. Because (x,y) (0,0) is top left, x positive is to the right and y positive is down from that point we are working with a flipped vertical plane. If you flip vertical your images you will understand the boolean too, here are the your flipped examples:
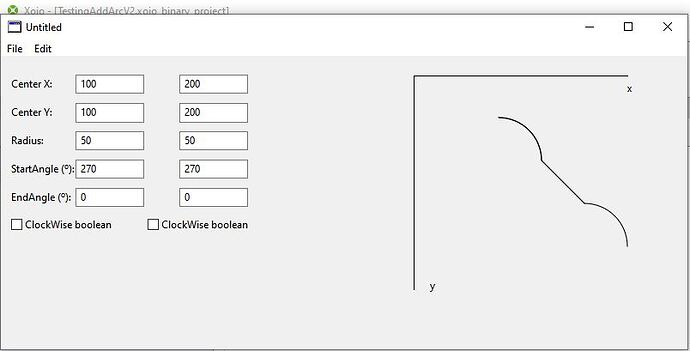
Your example 1:
Start at 0, clockwise True end at 90 then move to start in 90, clockwise False, end in 0
Your example 2:
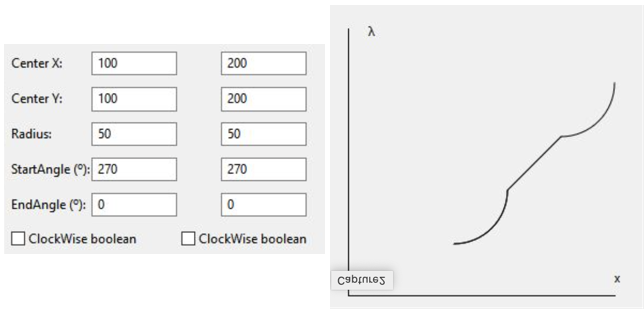
Start at 270, clockwise False, end at 0 move to start 270, clockwise false end at 0
As I said before, invert the boolean and you will get the result you need.
There is a bug either in the implementation or the documentation regarding the boolean parameter of the AddArc method.
Yes, this helps understanding where the origin of the issue may be, but anyway if we stick to the documentation (including the top-left as origin for the reference system) the rotation direction is wrong.
For me the rotation is wrong because we are looking at a flipped area, if we flip it vertically then it is writing as it should.
Sorry is hard to explain so for sure is not easy for people just starting with programming and used to work with a different Y.
With the images, I’m trying to illustrate how that ClockWise and counter ClockWise are working.
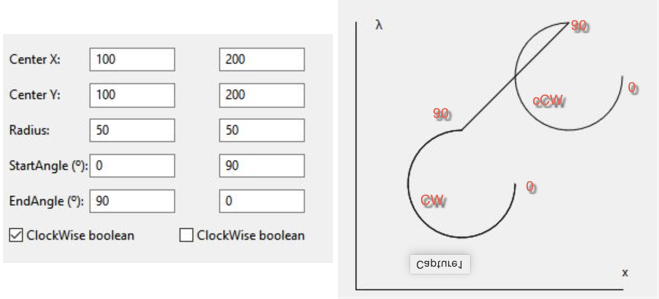
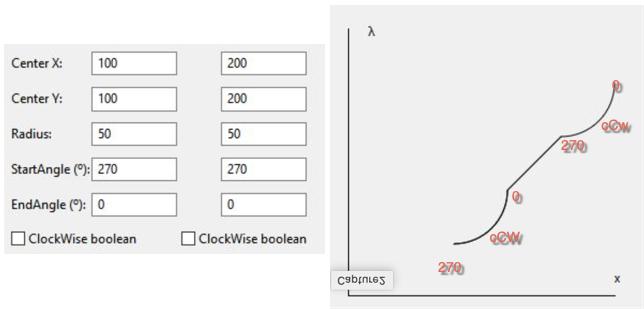
So it looks like the system is working as designed, as far as I understand this.
It makes sense from the point of view of the windows manager and the fact that a lot of what is going on in windows is the drawing of text which is referenced to the upper left corner. That, combined with the fact that the original windows had the resize control at the lower right, would have made the graphics routines very messy if they tried to use the standard mathematical convention.
In order to keep my sanity, I learned a long time ago to do all of my graphical calculations in standard Cartesian coordinates, and only do the final conversion when drawing the shape.
eg:
g.DrawLine(x1,g.height-y1,x2,g.height-y2)If the drawing direction is the intended one (which I doubt, but let’s say it is), then the documentation is wrong, because a true for the clockwise parameter results in an arc that is drawn counterclockwise on the canvas. The documentation should state that the drawing will happen towards positive angles when the boolean is true.
But, I think the implementation is wrong and the documentation right, that makes the most sense to me.
I get what you mean, but actually Xojo’s referense system is a standard cartesian coordinate system, only that instead of looking at the OXY plane from above (from a positive Z) we are looking at it from below (from a negative Z).
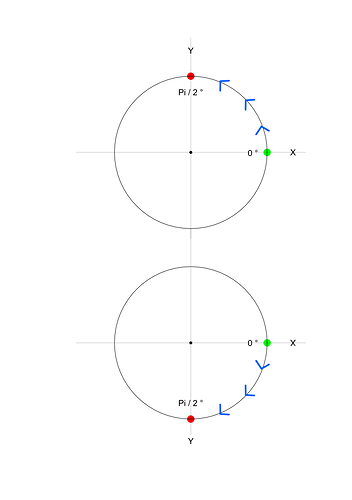
Command some non-computer high school student to draw an arc starting at 0° and going to Pi / 2°. The default coordinate system is as in seen in the upper drawing: Y increases toward the top and X to the right. Now ask the student did he draw clockwise or counter-clockwise? The answer will be counter-clockwise. He went from the green circle to the red circle and that was counter-clockwise. That is a fundamental truth of the mathematical universe.
Now you move into the “weird” computer world where 0,0 is in the left upper corner. Why is Pi / 2 shown as down now? It is not a Y value specifically, it is an angle. And yet it is shown down. And you might say that to get from 0° to Pi / 2° you go clockwise. But the student knows that that is not really correct. To start at 0° and go to Pi / 2° you go counter-clockwise as we have already established. Why should THAT change just because the y axis greater values are lower on the screen.
As people have suggested, think of the point of view of looking at the graph as if your eye is in a negative Z location. Then everything “works”. Look up at the graph and it looks like any graph we drew as students.
I am being a little glib here. I would have made the same assumption that Taz did when first encountering the documentation. But I can see the argument that the documentation is actually “correct” in some sense. If the convention for centuries has been that going from 0 degrees to 90 degrees is to go counterclockwise, why would we change it? Accept that when you are looking at a computer coordinate system your are looking from the wrong direction and switch your mind so that you are looking up at the graph and your eye is underneath it.
I think we are missing my specific problem here… the link line was not linking the end with the start… I am simulating every combination of flipping axes etc but none shows the endpoints linking correctly (while set to correct rotation).
The documentation states that the end of arc segment one links to the start of arc segment two. Also that clockwise is clockwise, obviously.
End of the day, the axis orientation doesn’t affect the rotation direction, clockwise is always clockwise. If we switch the start-end, sure we can make it look right, but then the stated direction is always incorrect.
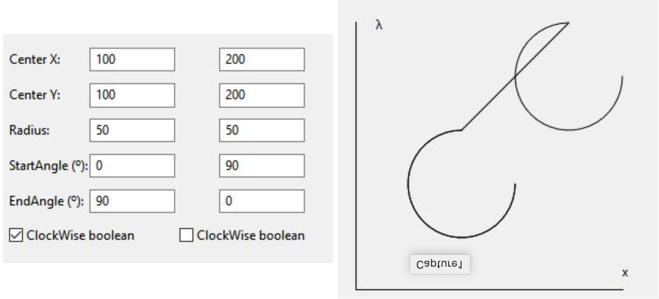
Here is my flipper preview, the grey curves are the default presentation. Try to put the settings to something where the directions are correct and the joining is correct… The only time I swap the start/end is when the flip checkbox is ticked.
Please tell me if I have a mistake in my simulation, as I said, I am a novice here.
Sorry Robert, I read your response after posting my latest… I have one basic difficulty wiht that, in that I am not talking pixels here, so cartesian conventions don’t come into it. My problem is the conflict between the boolean terms and the start/end terms which is causing my joins to not match, so you need to consider two arcs to see my problem.
The problem is that I want to join ends correctly with the rotation reading correctly.
Sure I can just reverse the the terms clockwise and anti-clockwise, but why?
The app natively puts 0 middle right and 90 bottom. So 0 - 90 is clockwise. In flipping the cartesian axes, the rotation may flip, but it always contradicts the stated boolean value as far as I can see.
Thankyou for taking the time to respond.
Alberto also…
Now ask the same question of a mariner, for whom 0º is North, 90º is East and and for an arc from North round to East, you draw clockwise, not anticlockwise. This is a different fundamental truth.
Dang… I can’t put my problem clearly.
Fair enough. But I would just say that Xojo does not use the mariner worldview. Xojo uses the worldview of the classic cartesian system that is taught in high school. If I am familiar with that system I have, at worst, a way to remember what Xojo considers the direction to be going from 0° to 90° and making the “small” arc. That direction is counter-clockwise.
Give me any two angles: a starting angle and a finishing angle. Now ask me to draw an arc between them. I might ask: do you want the short arc or the long arc? Whatever you say, I can easily visualize the answer because I am familiar with the classic cartesian conventions and it happens that Xojo uses them. The short arc between 0° and 90° is counter-clockwise. Consider it a mnemonic if you wish.
If you are not familiar with the classic cartesian conventions it will not be helpful. If you are really familiar with the mariner world then you could just remember that Xojo is the opposite of what mariners think.
But there is a certain consistency of the cartesian system. You might say that graphics on a computer are weird in two ways.
- Greater Y values are further down the screen
- Going from 0° to 90° on the short arc is clockwise.
But others would argue (as I would) that these are related. They are not independent of each other. As some other poster commented, think of looking at your graph from underneath. Then both these “anomalies” go away. They are manifestations of the same basic phenomena.
Phil seems to be content that 90° is “down” from 0° but is not happy that to get from 0° to 90° you go clockwise.
I am not happy that 90° is down and that big values of Y are down and, as he would have it, getting from 0° to 90° you go clockwise. You can get a consistent version of all these issues by imagining that you are looking at the graph from underneath it. All these things “go away” and the world is as it is in the cartesian mathematical convention.
I make the suggestion to Phil that he use the cartesian convention as a mnemonic when trying to figure out whether Xojo considers this arc to be clockwise or counterclockwise. It is “consistent” and “reliable”; it will always return the Boolean that is necessary.
If that does not work for him, fine. If he is not familiar/comfortable with the cartesian convention of where 0° and 45° and 90° and 180° are, then my suggestion is worthless for him.
Robert and Tim, you are both obsessed with the cartesian issue, that is not the problem here… I am happy to go up to 90 or down to 90 clockwise or anticlockwise!
The problem is that if you have 2 arcs, the end of one will NOT connect with the start of the other with Boolean matching the rotation direction. From the Start to the End (as defined by which end joins to the next arc) the terms will contradict, regardless of the axes.
No pixel calculation involved!
If you look at my demo, you will see the problem.