This. The list isn’t going to change. And access will be very fast.
The Sieve of Eratosthene interests me since it was commonly used as a computer benchmark back in the 80s.
What would be the fastest method, other than iterating each row of the array and testing for true values?
@Kem_Tekinay’s suggestion of putting the primes in their own array makes sense, is probably fastest and is what is also recommended on the wikipedia page’s pseduo-code.
return all i such that A[i] is true.
For fun I made a quick method:
Public Function Sieve(maxNum As Integer) As Integer()
// https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes
Var nums() As Boolean
nums.ResizeTo(maxNum)
Var j As Integer
Var cnt As Integer
Var max As Integer = Sqrt(maxNum)
For i As Integer = 2 To max
If nums(i) = False Then
j = i*i
cnt = 0
While j <= maxNum
nums(j) = True
j = i*i + cnt * i
cnt = cnt + 1
Wend
End If
Next
Var primes() As Integer
For i As Integer = 2 To nums.LastIndex
If nums(i) = False Then
primes.Add(i)
End If
Next
Return primes
End Function
These are my results in an app built with Aggressive optimization (i7 Mac mini):
Benchmarking is fun!
By adding this one line to your Sieve function
#Pragma DisableBackgroundTasks
I get roughly a 4x speedup at lower numbers, and 2x at higher (at Default compiler optimization):
And with Aggressive optimization (i7 2019 macbook pro) a little better:
Wow, the M1 mac mini is about 2x to 3x as fast:
Many thanks to all replyers, for help, suggestions and benchmarks.
I finally tried searching for results in a array with IndexOf, that is very fast. It finds the last Prime of 50847534 in a array of one billion rows in 2-3 secondes. So, dictionary no longer needed…
My own results on iMac I7 2.8 GHz End 2009, 16 GB RAM, with aggressive optimization:
1 000 000 integers, 74 498 Primes found in 0.0525981
10 000 000 integers, 664 579 Primes found in 0.5831727 seconds
100 000 000 integers, 5 761 455 Primes found in 6.266525 seconds
1 000 000 000 integers, 50 847 534 Primes found in 66.777 seconds
Using #Pragma DisableBackgroundTasks:
1 000 000 integers, 74 498 Primes found in 0.0144943
10 000 000 integers, 664 579 Primes found in 0.1863138 seconds
100 000 000 integers, 5 761 455 Primes found in 2.437393 seconds
1 000 000 000 integers, 50 847 534 Primes found in 27.73094 seconds
That is, about 3x to 2.5x faster.
Great to hear.
Please remember to pick a post as a solution.
this change makes a lot of speed difference since array.add is so slow:
Var primes() As Integer
primes.ResizeTo(maxNum)
j=0
For i As Integer = 2 To nums.LastIndex
If not nums(i) Then
primes(j)=i
j=j+1
End If
Next
primes.ResizeTo(j)
Return primes
Indeed, Array.Add() is quite slow. With that change, I now get the following speeds:
Intel (i7)
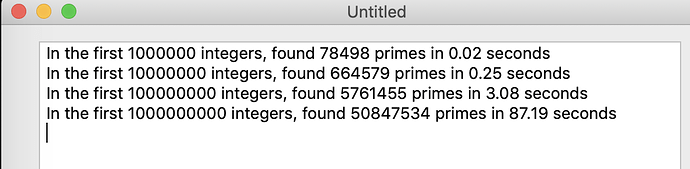
In the first 1000000 integers, found 78499 primes in 0.02 seconds
In the first 10000000 integers, found 664580 primes in 0.12 seconds
In the first 100000000 integers, found 5761456 primes in 1.9 seconds
In the first 1000000000 integers, found 50847535 primes in 18.97 secondsWhy now it says “found 78499” when previous images show “found 78498”?
Well, all are 1 more than before.
Edit: ah, is the resize to j the problem, maybe use primes.ResizeTo(j-1)
Result windows 10 AMD Ryzen 5 1600x base-clock 3.60Ghz (mem speed 2133mhz):

These results are from the Build application with “Aggresive” optimization
Code a little modified:
Public Function Sieve(maxNum As Integer) As Integer()
// https://en.wikipedia.org/wiki/Sieve_of_Eratosthenes
#Pragma BackgroundTasks False
#Pragma StackOverflowChecking False
#Pragma NilObjectChecking False
#Pragma BoundsChecking False
#Pragma BreakOnExceptions False
Var nums() As Boolean
nums.ResizeTo(maxNum)
Var i, j, cnt As Integer
Var max As Integer = Sqrt(maxNum)
Var primes() As Integer
Var primesCount As Integer = 0 // The actual count that will be returned (see bottom)
primes.ResizeTo(max)
For i = 2 To max
If nums(i) = False Then
j = i*i
cnt = 0
While j <= maxNum
nums(j) = True
j = (i * i) + (cnt * i)
cnt = cnt + 1
Wend
End If
Next
Var lastNumsIndex As Integer = nums.LastIndex
primes.ResizeTo(nums.LastIndex)
For i = 2 To lastNumsIndex
If nums(i) = False Then
primesCount = primesCount + 1
primes(primesCount-1) = i
End If
Next
primes.ResizeTo(primesCount-1)
Return primes
End FunctionThis runs in about 8s here (1 billion):
Public Function FindPrimes(thruValue As Integer) as Integer()
#if not DebugBuild
#pragma BackgroundTasks false
#pragma BoundsChecking false
#pragma NilObjectChecking false
#pragma StackOverflowChecking false
#endif
dim result() as Integer
if thruValue < 2 then
return result
end if
result.ResizeTo thruValue / 10 + 2
var resultIndex as integer = -1
dim notPrime() as boolean
redim notPrime( thruValue )
//
// We know the status of 0, 1, and 2 so
// check the rest
//
dim thruValueSqrt as integer = ( thruValue + 1.0 ) ^ 0.5
for checkValue as Integer = 3 to thruValueSqrt step 2
if notPrime( checkValue ) then
//
// If this value was already identified,
// so were all of its "children"
//
continue for checkValue
end if
dim stepper as Integer = checkValue + checkValue
dim firstValue as Integer = checkValue * checkValue
for i as Integer = firstValue to thruValue step stepper
notPrime( i ) = true
next i
next checkValue
//
// Add 2
//
resultIndex = resultIndex + 1
result( resultIndex ) = 2
for i as Integer = 3 to thruValue step 2
if notPrime( i ) = false then
resultIndex = resultIndex + 1
if resultIndex > result.LastIndex then
result.ResizeTo( resultIndex + resultIndex )
end if
result( resultIndex ) = i
end if
next i
result.ResizeTo resultIndex
return result
End Function
thank you ! Neat trick to balance performance between search through an array of given size versus array.resizeTo 
Nice, got this result on the AMD Ryzen 5 1600x windows 10
Starting benchmark
SIEVE - 78498 primes in loops 1000000 took: 0.000000
FindPrimes - 78498 primes in loops 1000000 took: 0.015000
SIEVE - 664579 primes in loops 10000000 took: 0.125000
FindPrimes - 664579 primes in loops 10000000 took: 0.058000
SIEVE - 5761455 primes in loops 100000000 took: 1.581000
FindPrimes - 5761455 primes in loops 100000000 took: 0.782000
SIEVE - 50847534 primes in loops 1000000000 took: 17.804000
FindPrimes - 50847534 primes in loops 1000000000 took: 8.835000
Ended benchmark
Nice read. Some good tips here, thank you all.
Looking forward to compare these results with an M1 chip 
FYI, there was quite a lively discussion on the sieve algorithm about 4 years ago here:
https://forum.xojo.com/t/algorithm-puzzle-challenge-xojo-vs-c-vs-python/38238
Good job and well done, Kem!
I believe optimization is on its max! 
M1 Macbook Air - ARM64 Aggressive Build
SIEVE
In the first 1000000 integers, found 78498 in 0.0081687 seconds
In the first 10000000 integers, found 664579 in 0.0850987 seconds
In the first 100000000 integers, found 5761455 in 1.0328279 seconds
In the first 1000000000 integers, found 50847534 in 11.0918392 secondsFIND PRIMES
In the first 1000000 integers, found 78498 in 0.0028872 seconds
In the first 10000000 integers, found 664579 in 0.0289305 seconds
In the first 100000000 integers, found 5761455 in 0.4544424 seconds
In the first 1000000000 integers, found 50847534 in 5.3206291 seconds
Blockquote
In the first 1000000000 integers, found 50847534 in 5.3206291 seconds
Blockquote
Very impressive, given that my first try took about … 300 seconds!
Now, it takes 17 seconds on iMac later 2009, 2.8 GHz.